Deep Learning
“Deep Learning” beschreibt das Teilgebiet des maschinellen Lernens, das sich mit neuronalen Netzen beschäftigt.
Simple Mathematik \[ \small \begin{aligned} \begin{pmatrix} W_{11} & W_{12} & \cdots & W_{1j}\\ W_{21} & W_{22} & \cdots & W_{2j}\\ \vdots & \vdots & \ddots & \vdots\\ W_{i1} & W_{i2} & \cdots & W_{ij}\\ \end{pmatrix} \end{aligned} \]
Gefährliche Künstliche Intelligenz \[ \small \begin{aligned} \begin{pmatrix} W_{11} & W_{12} & \cdots & W_{1j}\\ W_{21} & W_{22} & \cdots & W_{2j}\\ \vdots & \vdots & \ddots & \vdots\\ W_{i1} & W_{i2} & \cdots & W_{ij}\\ \end{pmatrix} \cdot \begin{pmatrix} W_{11} & W_{12} & \cdots & W_{1k}\\ W_{21} & W_{22} & \cdots & W_{2k}\\ \vdots & \vdots & \ddots & \vdots\\ W_{j1} & W_{j2} & \cdots & W_{jk}\\ \end{pmatrix} \cdot \begin{pmatrix} W_{11} & W_{12} & \cdots & W_{1l}\\ W_{21} & W_{22} & \cdots & W_{2l}\\ \vdots & \vdots & \ddots & \vdots\\ W_{k1} & W_{k2} & \cdots & W_{kl}\\ \end{pmatrix} \cdot \begin{pmatrix} W_{11} & W_{12} & \cdots & W_{1m}\\ W_{21} & W_{22} & \cdots & W_{2m}\\ \vdots & \vdots & \ddots & \vdots\\ W_{l1} & W_{l2} & \cdots & W_{lm}\\ \end{pmatrix} \end{aligned} \]
Lies weiter, wenn du Lust auf ein bisschen Mathe hast. 🤓
Neuronale Netze
Intuitive Erklärung Neuronaler Netze
[Adaptiert von: “AI for everyone” von Andrew Ng (coursera.org)]
Angenommen, wir haben einen Online-Shop und versuchen vorherzusagen, wie viel wir von einem Produkt im nächsten Monat verkaufen werden. Der Preis, zu dem wir bereit sind, das Produkt anzubieten, beeinflusst offensichtlich die Nachfrage, da die Leute versuchen, ein gutes Geschäft zu machen, d.h. je niedriger der Preis, desto höher die Nachfrage. Es handelt sich um eine negative Korrelation, die durch ein lineares Modell beschrieben werden kann. Die Nachfrage ist jedoch nie kleiner als Null (d.h. wenn der Preis sehr hoch ist, werden die Kunden das Produkt nicht plötzlich zurückgeben), also müssen wir das Modell so anpassen, dass der vorhergesagte Output nie negativ ist. Dies erreichen wir durch eine Max-Funktion (in diesem Zusammenhang auch nichtlineare Aktivierungsfunktion genannt), die auf das Ergebnis des linearen Modells angewendet wird, sodass wenn das lineare Modell einen negativen Wert berechnet stattdessen 0 vorhergesagt wird.
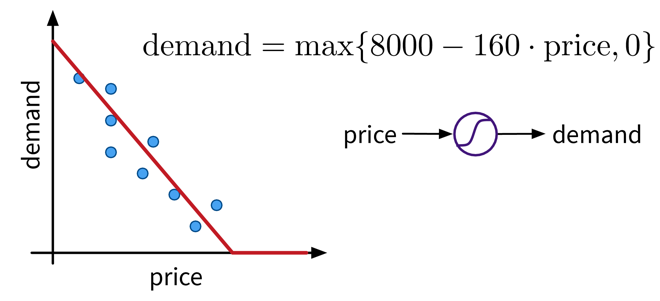
Diese funktionale Beziehung kann auch als Kreis mit einem Input (Preis) und einem Output (Nachfrage) visualisiert werden, wobei die S-Kurve im Kreis anzeigt, dass auf das Ergebnis eine nichtlineare Aktivierungsfunktion angewendet wird. Wir werden dieses Symbol später als einzelne Einheit oder “Neuron” eines neuronalen Netzes (NN) sehen.
Um die Vorhersage zu verbessern, können wir das Modell erweitern und mehrere Input Features für die Vorhersage verwenden:
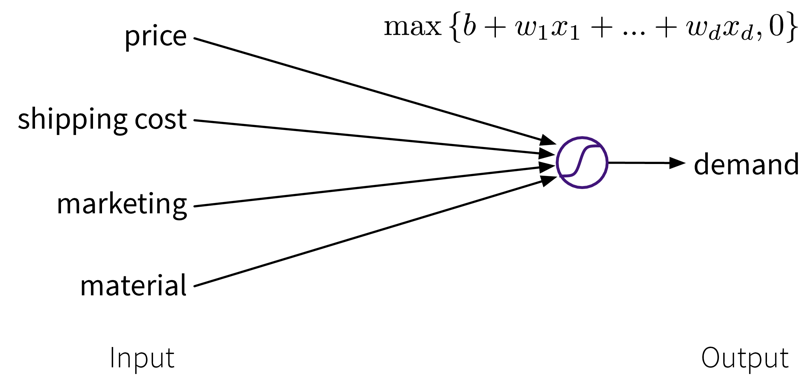
Um die Performance des Modells noch weiter zu verbessern, können wir aus den ursprünglichen Inputs manuell informativere Features generieren, indem wir sie sinnvoll kombinieren (→ Feature Engineering), bevor wir den Output berechnen:
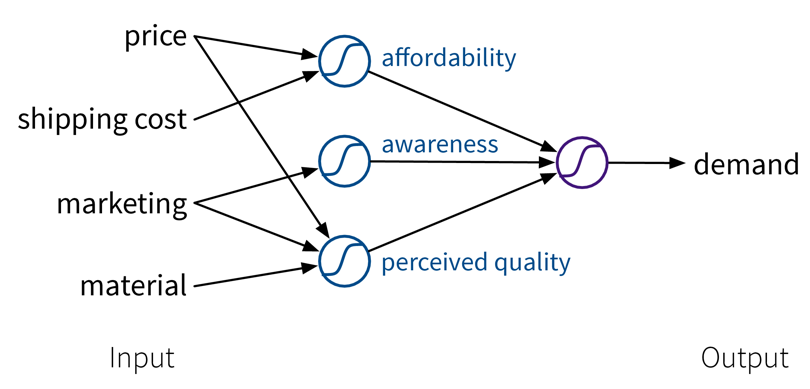
Während es in diesem Anschauungsbeispiel möglich war, solche Features manuell zu konstruieren, ist das Vorteilhafte an neuronalen Netzen, dass sie genau das automatisch tun: Indem wir mehrere Zwischenschichten (Layers) verwenden, d.h. mehrere lineare Modelle (mit nichtlinearen Aktivierungsfunktionen) verbinden, werden immer komplexere Kombinationen der ursprünglichen Input Features generiert, die die Performance des Modells verbessern können. Je mehr Layers das Netzwerk verwendet, d.h. je “tiefer” es ist, desto komplexer sind die resultierenden Feature Repräsentationen.
Da verschiedene Problemstellungen und insbesondere verschiedene Arten von Input Daten von unterschiedlichen Feature Repräsentationen profitieren, gibt es verschiedene Arten neuronaler Netzarchitekturen, um diese aussagekräftigeren Zwischenfeatures zu berechnen, z.B.
- Feed Forward Neural Networks (FFNNs) für ‘normale’ (z.B. strukturierte) Daten
- Convolutional Neural Networks (CNNs) für Bilder
- Recurrent Neural Networks (RNNs) für sequenzielle Daten wie Text oder Zeitreihen
NN Architekturen
Ähnlich wie domänenspezifisches Feature Engineering zu erheblich verbesserten Modellvorhersagen beitragen kann, lohnt es sich gleichermaßen, eine auf die jeweilige Aufgabe zugeschnittene neuronale Netzwerkarchitektur zu konstruieren.
Feed Forward Neural Network (FFNN)
Das FFNN ist die ursprüngliche und einfachste neuronale Netzwerkarchitektur, die auch im ersten Beispiel verwendet wurde. Allerdings bestehen diese Modelle in der Praxis normalerweise aus mehr Layers und Neuronen pro Layer:
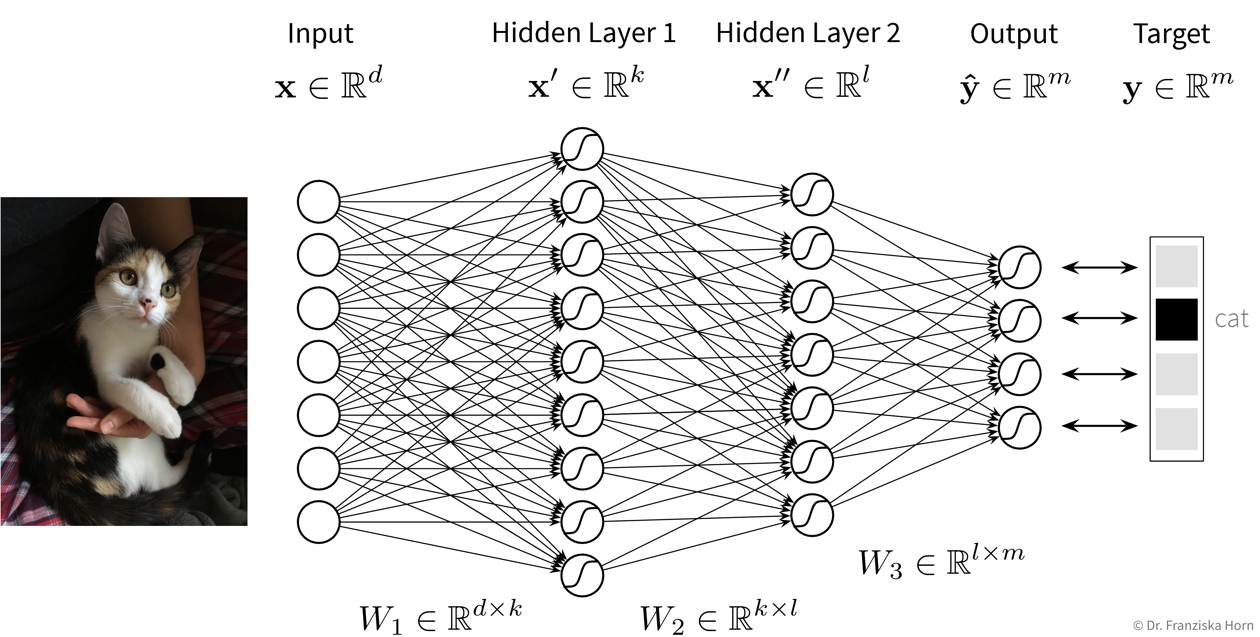
Du kannst hier auch selbst mit einem kleinen neuronalen Netz herumspielen um z.B. zu schauen wie es sich verhält wenn du mehr Neuronen oder Layers verwendest.
Convolutional Neural Network (CNN)
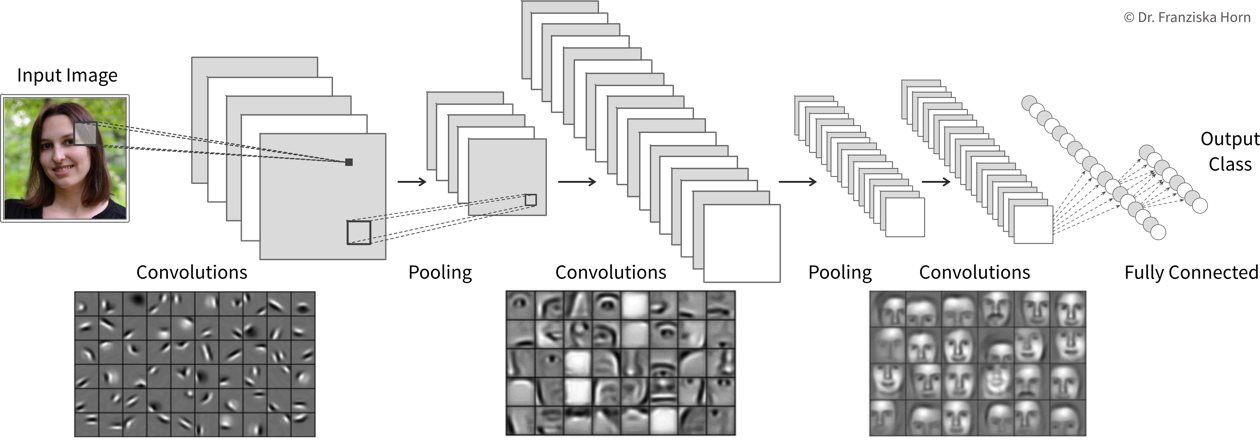
Manuelles Feature Engineering für Computer Vision Aufgaben ist sehr schwierig. Während der Mensch mühelos eine Vielzahl von Objekten in Bildern erkennt, ist es schwer zu beschreiben, warum wir erkennen was wir sehen, z.B. anhand welcher Merkmale wir eine Katze von einem kleinen Hund unterscheiden. Das Deep Learning hatte seinen ersten bahnbrechenden Erfolg auf diesem Gebiet, da neuronale Netze, insbesondere CNNs, es durch eine Hierarchie von Layern schaffen, sinnvolle Feature Repräsentationen aus visuellen Informationen zu lernen.
Convolutional Neural Networks eignen sich sehr gut für die Verarbeitung visueller Informationen, da sie direkt mit 2D-Bildern arbeiten können und die Tatsache nutzen, dass Bilder viele lokale Informationen beinhalten (z.B. sind Augen, Nase und Mund lokalisierte Komponenten eines Gesichts).
Allgemeine Prinzipien & fortgeschrittene Architekturen
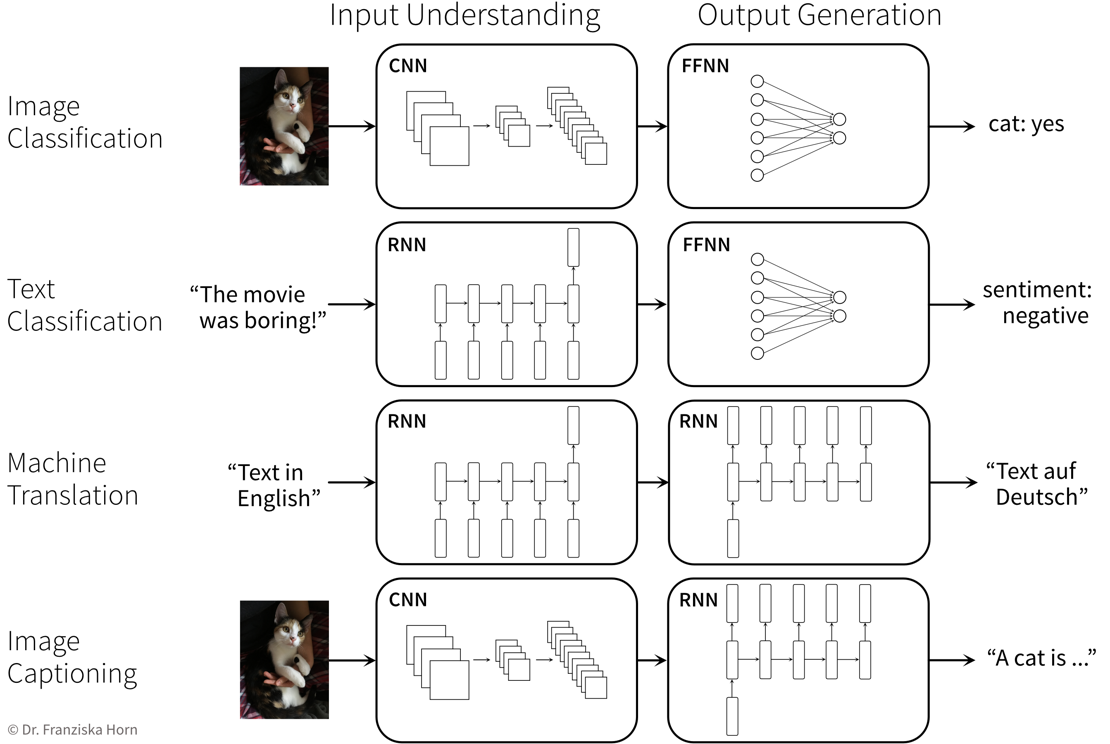
Bei der Lösung eines Problems mit einem NN muss man immer berücksichtigen, dass das Netzwerk sowohl die Input Daten verstehen als auch die gewünschten Ausgaben generieren muss: