Recommender Systems (Pairwise Data)
Recommender systems can be found on many websites to promote products, content, or ads that a specific user might be interested in (e.g., on Amazon, Netflix, Facebook, YouTube, etc.).
What is special about them is that here we’re not really dealing with single data points, but instead with pairwise data, i.e., we have samples from two groups (e.g., users and movies), where each combination of samples (e.g., each (user, movie)-tuple) is assigned a label (e.g., the rating the user gave to the movie).
Typically, the training set contains only very few labels (e.g., since there are many users and many movies, but every user has only rated a handful of movies) and the task is to predict all the missing labels, based on which then, for example, a user would be recommended the movie with the highest predicted rating.
Recommender Systems Overview:
- Pairwise data
-
-
(user, movie) → rating (1 - 5 stars)
-
(drug, protein) → bind (yes / no)
-
Idea: Similar users watch similar movies.
Given: Very sparse matrix with known interactions:
Task: Fill in the missing values.
There are lots of different approaches for how to accomplish this, and we’ll only look at two here, the traditional method of collaborative filtering, and a more modern approach relying on neural networks that falls under the category of triplet learning.
→ One possible Python library: surprise
- Collaborative Filtering
-
Using a singular value decomposition (SVD; basically the big sister of the eigendecomposition, e.g., from
scipy.sparse.linalg.svds), the matrix with the known interactions can be decomposed into two smaller matrices of shapes (number of movies \(\times\, d\)) and (\(d \,\times\) number of users) and by multiplying these matrices together, the missing values from the original matrix are approximated:
The two matrices we obtain from the SVD contain d-dimensional latent variable representations of movies and users respectively, where d denotes the number of eigenvectors we decided to keep (corresponding to the d largest eigenvalues of the original matrix). You can think of these as feature vectors, where, for example, one of the d dimensions in the vector representing a movie might correspond to how much this movie is considered a horror movie, while the same dimension in a user vector indicates how much this user likes horror movies. If both entries for some dimension in the vectors point in the same direction (e.g., the movie is a horror movie and the user likes horror movies), then the product of the two entries will contribute positively to the overall scalar product of the vectors and therefore the approximated rating. However, please note that just like with the new feature dimensions we got from PCA, it is very difficult to determine exactly what is actually encoded in each dimension.
One big problem with this approach is that we always need some initial ratings for each user and movie, otherwise we can’t generate any useful personalized recommendations. This is also referred to as the “cold start problem”, which can be addressed with triplet learning.
- Triplet Learning / Content-based Filtering
-
In triplet learning, we don’t directly work with the full matrix of known interactions, but instead the training dataset consists of triplets for the existing labels (e.g., (user i, movie j, 4 stars), which can also be a more memory-friendly representation). Additionally, we assume that we have feature vectors available for the users and movies (e.g., the users might have filled out a short survey when they set up an account and for the movies we know the genres, directors, and plot keywords; if all fails, this could also just be a one-hot encoding).
Given the two feature vectors of a user and a movie, we predict the interaction value directly: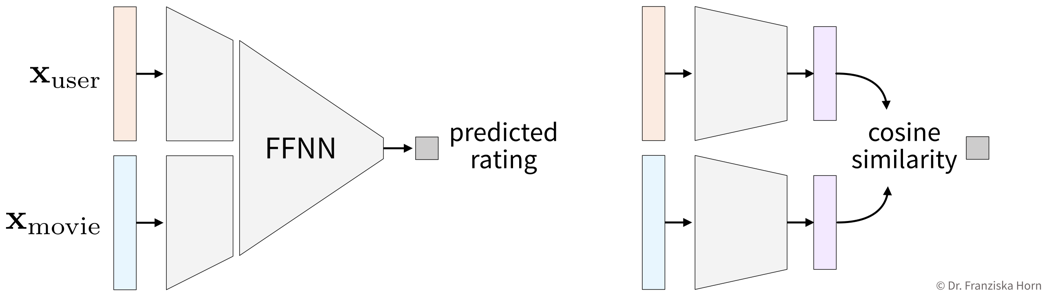
These are two possible neural network architectures for predicting the rating a user might give to a movie. The architecture on the left first processes the user and movie feature vectors individually (in case they require a certain type of network to be understood, e.g., for the movie plot description or poster), and then the representations are concatenated into a single vector, which is then passed to a FFNN to predict the rating (= a regression task). A different approach is shown on the right, where instead the two original feature representations for users and movies are projected into the same vector space, where then the cosine similarity of these two vectors is computed to predict the interaction between them (similar as with the d-dimensional latent variable representations in the collaborative filtering approach).→ Given the feature vector of a new user who has not rated any movies yet, we are now able to generate useful predictions.