Reinforcement Learning

Finally, we come to the last main category of ML algorithms besides unsupervised and supervised learning: reinforcement learning.

Main idea

Agent performs actions in some environment and learns their (state-specific) consequences by receiving rewards.

image
The environment lets the agent know in which state it currently is. Then the agent selects some action, i.e., how it responds to this state, according to its internal policy function \(\pi\) (the main thing that is learned in RL). The environment evaluates the consequences of this action and returns an immediate reward (e.g., "game over" or "collected a coin"), as well as the next state, at which point the cycle repeats.

Goal: Maximize the cumulative reward (also called return), i.e., the sum of the immediate rewards received from the environment over all time steps in an episode (e.g., one level in a video game).
The difficult thing here is that sometimes an action might not result in a big immediate reward, but is still crucial for the agent’s long-term success (e.g., finding a key at the beginning of a level and the door for which we need the key comes much later). This means the agent needs to learn to perform an optimal sequence of actions from delayed labels.

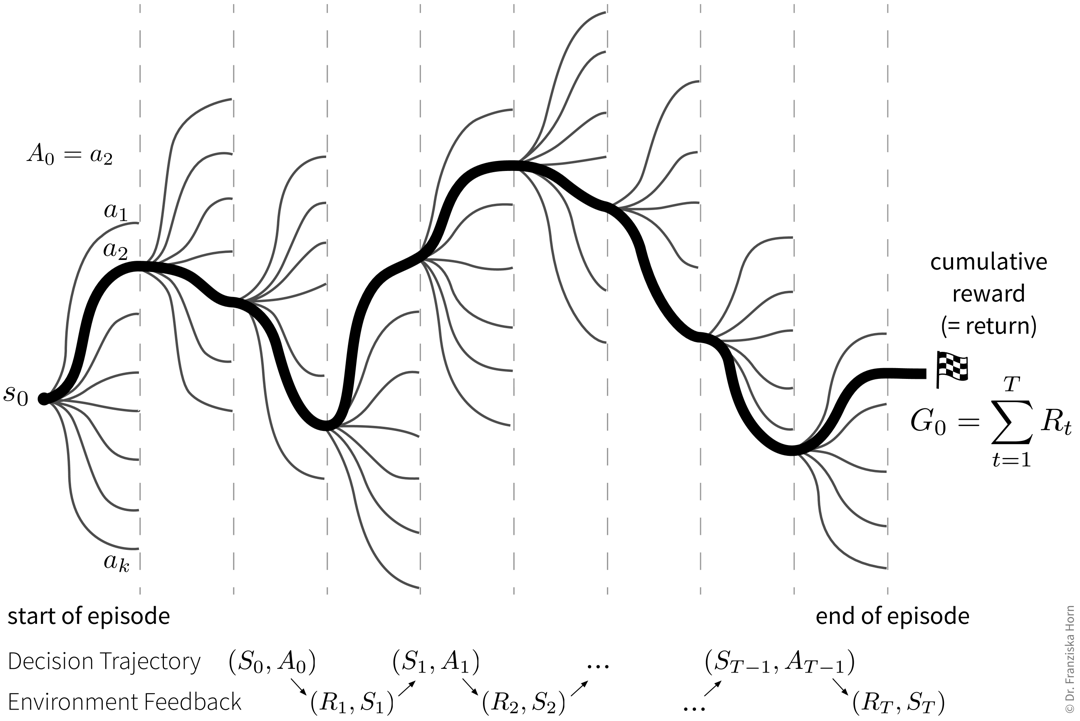
The agent’s decision trajectory basically defines one path among a bunch of different possible parallel universes, which is then judged in the end by the collected return:

image
Reinforcement Learning vs. ‘normal’ Optimization

In regular mathematical optimization, we are given some fixed function \(f: \mathbb{R}^d \to \mathbb{R}\) and try to find the inputs \(\mathbf{x} \in \mathbb{R}^d\) that maximize (or minimize) the value of \(f(\mathbf{x})\). Since each evaluation of \(f(\mathbf{x})\) is independent of the next, we could theoretically try as many different values for \(\mathbf{x}\) as we wanted, until we’ve found some combination of inputs that results in an optimal value for \(f\).
If \(f\) is easily differentiable, the solution to the optimization problem can be found analytically by setting the first derivative of \(f\) to zero to obtain the local extrema or saddle points of \(f\), which can then be examined further to determine the (global) maximum or minimum. If \(f\) is not differentiable (or very complicated), there exist other methods to find optimal values (for example, the gradient descent procedure used to tune the weights of neural networks is one method for obtaining a (local) optimum without calculating the derivative of the network’s error function directly, while a naive grid search, where we just try many different input combinations and then select the values with the best outcome, or more fancy approaches such as particle swarm optimization, can also be applied to functions that are non-differentiable).

Translated to RL terms, \(f\) would be the environment in one particular state, \(\mathbf{x}\) would be the action, and \(f(\mathbf{x})\) would be the immediate reward as a result of taking this action in the current state. However, since in RL setups the state of the environment changes with each action that is taken, this means the function \(f\) also changes in each step and an action that might have resulted in a high reward in the previous step could now mean “game over”. Furthermore, in RL we’re not too concerned about every single immediate reward, but instead we want to achieve long-term success, measured by the return (i.e., cumulative rewards), and an action with a low immediate reward might still pay off later.

Immediate rewards vs. long-term value of states

To make decisions that are good in the long run, we’re more interested in what being in a state means w.r.t. reaching the final goal instead of receiving immediate rewards:

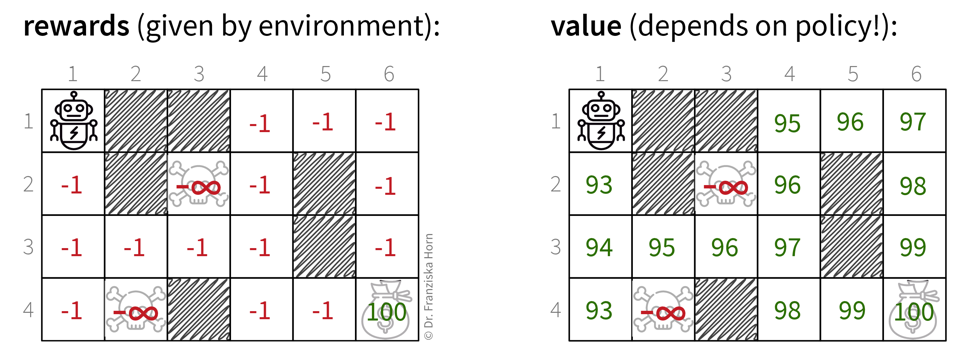image
Left: This is a simple "grid world", where an agent can move up, down, left, or right through the states. This small environment contains three terminal states (i.e., when the agent reaches one of them, the episode ends): Two states mean "game over" with an infinite negative reward, while reaching the state in the lower right corner means receiving a large positive immediate reward. When the agent resides in any of the other (reachable) states, it receives a small negative reward, which is meant to "motivate" the agent to go to the goal state as quickly as possible. However, knowing only the immediate reward for each state is not very helpful to decide which action to take next, since in most states, the reward for moving to any of the surrounding states or staying in place would be the same. Therefore, what the agent needs to learn in order to be able to choose an action in each state that has the potential of bringing it closer to the goal state, is the value of being in each state. Right: The value of a state is the expected return when starting from this state. Of course, the expected return is highly dependent on the agent’s policy \(\pi\) (i.e., the actions it takes), e.g., if the agent would always move to the left, then it would never be able to reach the goal, i.e., the expected return starting from any state (except the goal state itself) would always be negative. If we assume an optimal policy (i.e., the agent always takes the quickest way to the goal), then the value of each state corresponds to the ones shown in the graphic, i.e., for each state "100 minus the number of steps to reach the goal from here". Knowing these values, the agent can now very easily select the best next action in each state, by simply choosing the action that brings it to the next reachable state with the highest value.

The value of a state \(s\) corresponds to the expected return \(G_t\) when starting from state \(s\):

\[V^\pi(s) = \mathbb{E} [G_t | S_t = s]\]

The most naive way to calculate \(V^\pi(s)\) would be to let the agent start from this state several times (depending on how complex the environment is usually several thousand times), observe how each of the episodes play out, and then compute the average return that the agent had received in all these runs starting from state \(s\).

Similarly, we can calculate the expected return when executing action \(a\) in state \(s\):

\[Q^\pi(s, a) = \mathbb{E} [G_t | S_t = s, A_t = a]\]

I.e., here again we could let the agent start from the state \(s\) many times, but this time the first action it takes in this state is always \(a\).

Exploration/Exploitation trade-off

Of course, it would be very inefficient to always just randomly try out actions in any given state and thereby risk a lot of predictable “game over”. Instead, we want to balance exploration and exploitation to keep updating our knowledge about the environment, but at the same time also maximize the rewards collected along the way. This is again inspired by human behavior:

  • → Exploration: Learn something about the environment (e.g., try a new restaurant).

  • → Exploitation: Use the collected knowledge to maximize your reward (e.g., eat somewhere you know you like the food).

A very simple strategy to accomplish this is the Epsilon-Greedy Policy:

initialize eps = 1
for step in range(max_steps):
    if random(0, 1) > eps:
        pick best action (= exploitation)
    else:
        pick random action (= exploration)
    reduce eps
Tabular RL: Q-Learning

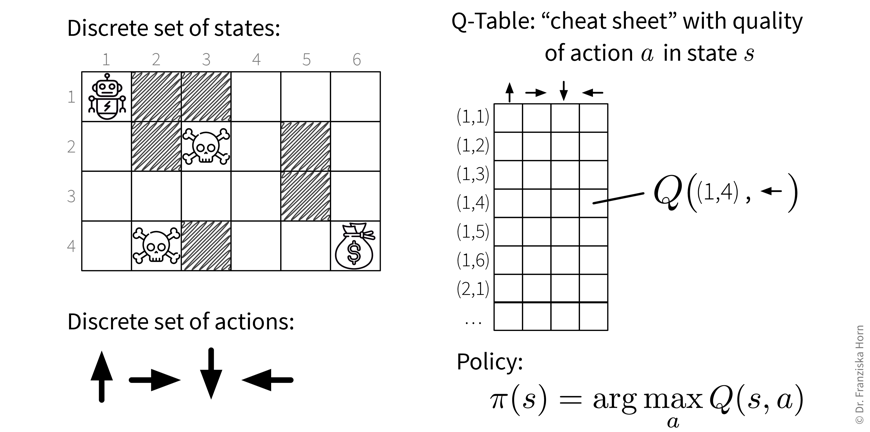
This brings us to the simplest form of RL, tabular RL, where an agent has a finite set of actions to choose from and operates in an environment with a finite set of states (like the grid world from above). Here, we could simply compute the Q-value for each (state, action)-combination as described above, and save these values in a big table. This so-called Q-table then acts as a cheat sheet, since for each state the agent is in, it can just look up the Q-values for all of the available actions and then choose the action with the highest Q-value (when in exploitation-mode):

image
Function Approximation: Deep Q-Learning

Unfortunately, almost no practical RL application operates in an environment consisting of a finite set of discrete states (and sometimes even the agent’s actions are not discrete, e.g., the steering wheel positions in a self-driving car — but this goes too far here). In video games, for example, each frame is a new state and depending on the complexity of the game, no two frames might be exactly alike. This is where Deep Q-Learning comes in:

Given a state \(s\) (represented by a feature vector \(\mathbf{x}_s\)), predict the Q-value of each action \(a_1 ... a_k\) with a neural network:

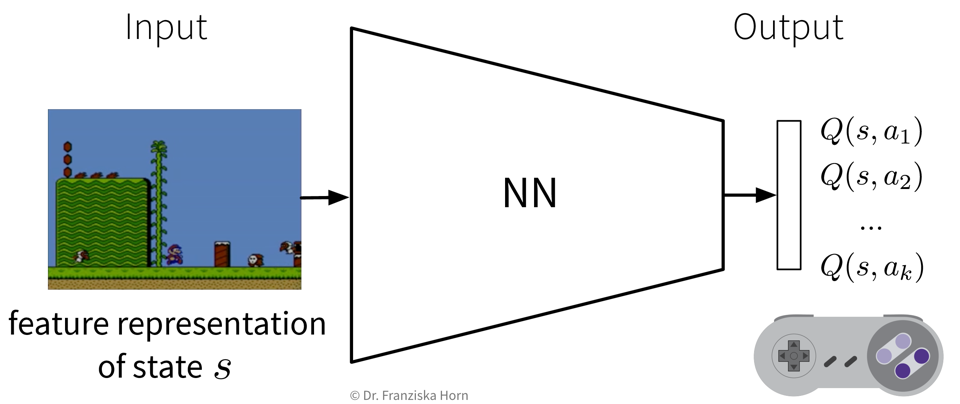
image

This can be seen as a direct extension of the tabular Q-learning: If we represented our states as one-hot encoded vectors and used a linear network with a single weight matrix that consisted of the Q-table we had constructed before, by multiplying the one-hot encoded vector with the Q-table, the network would “predict” the row containing the Q-values for all actions in this state.
By using a more complex network together with meaningful feature representations for the states, deep Q-learning enables the agent to generalize to unseen states. However, just like in time series forecasting tasks, here again the feature representation of a state needs to include all the relevant information about the past, e.g., in video games (think: old pong game) the feature vector could contain the last four frames to additionally capture the direction of movement.

Pros

  • RL works well for games:
    → Environment = Game = Simulation (i.e., no discrepancy between “real world” and simulation model).
    → Well defined reward function.
    → Utilize “self-play” for multi-player games, i.e., two RL agents playing against each other.

Careful

  • Acting in the real world is too expensive → need accurate (simulation) model of the environment.

  • AIs love to cheat and exploit bugs in the simulation.

  • Difficult to design appropriate reward function (and RL will overfit it, resulting in unintended consequences).

  • Model-free RL is very sample inefficient (i.e., needs millions of iterations, which takes too long in real-time).

  • Agent is responsible for collecting its own experiences: bad policy ⇒ bad data ⇒ no improvement.

  • Deep RL: complex network architectures, very sensitive to hyperparameter choices
    ⇒ Hard to train & get robust results → requires lots of tricks.

→ Imitation learning is often used instead of RL, which just means using supervised learning to train an agent to react similar to a human in some situation. Often, it is also easier to collect data from humans than to define a complicated reward function, e.g., humans drive around all the time, however, it is hard to define what would be considered “good driving” under lots of different circumstances. After the agent was pretrained on the human behavior, its policy can still be fine-tuned with an RL approach (e.g., this is how AlphaGo became better than a human Go master).

RL further reading + videos

General theory:

Words of caution (recommended for everyone):

RL in action:

← Previous: Time Series Forecasting | ↑ Up: Advanced Topics | ⌂ Home: A Practitioner’s Guide to Machine Learning | Next: Conclusion →