A Practitioner’s Guide to Machine Learning

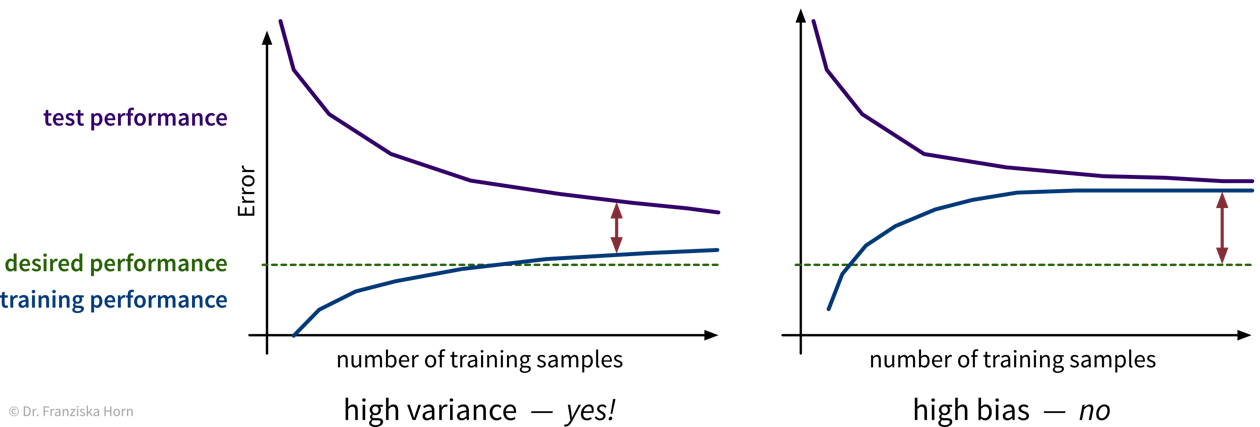
Model does not generalize

We want a model that captures the ‘input → output’ relationship in the data and is capable of interpolating, i.e., we need to check:
Does the model generate reliable predictions for new data points from the same distribution as the training set?

While this does not ensure that the model has actually learned any true causal relationship between inputs and outputs and can extrapolate beyond the training domain (we’ll discuss this in the next section), at least we can be reasonably sure that the model will generate reliable predictions for data points similar to those used for training the model. If this isn’t given, the model is not only wrong, it’s also useless.

Over- & Underfitting

So, why does a model make mistakes on new data points? A poor performance on the test set can have two reasons: overfitting or underfitting.

If we only looked at the test errors for the different models shown here, we could conclude that the model on the left (overfitting) and the one on the right (underfitting) are equally wrong. While this is true in some sense, the test error alone does not tell us why the models are wrong or how we could improve their performance. As we can see, the two models make mistakes on the test set for completely different reasons: The model that overfits, memorized the training samples and is not able to generalize to new data points, while the model that underfits is too simple to capture the relationship between the inputs and outputs in general.

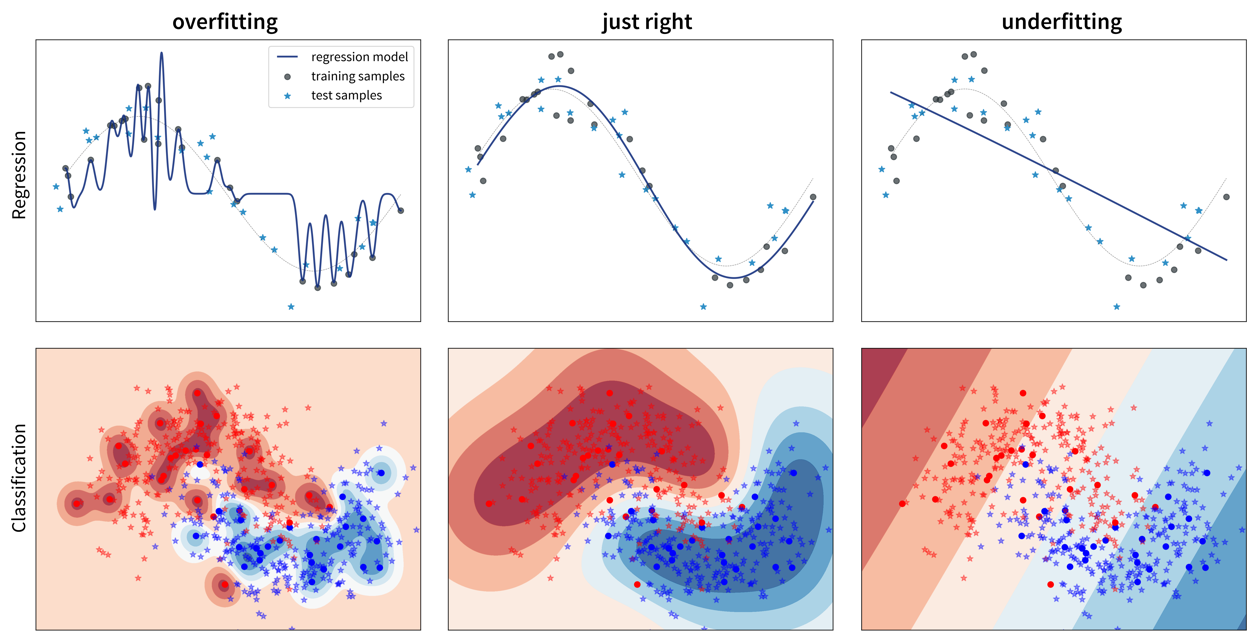
These two scenarios require vastly different approaches to improve the model’s performance.

Since most datasets have lots of input variables, we can’t just plot the model like we did above to see if it is over- or underfitting. Instead we need to compute the model’s prediction error with a meaningful evaluation metric for both the training and the test set and compare the two to see if we’re dealing with over- or underfitting:

Overfitting: great training performance, bad on test set
Underfitting: poor training AND test performance

Depending on whether a model over- or underfits, different measures can be taken to improve its performance:

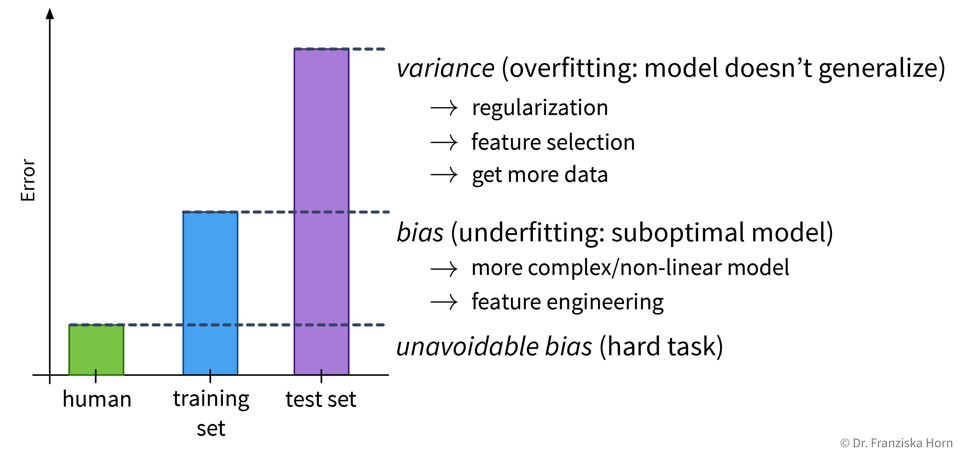
However, it is unrealistic to expect a model to have a perfect performance, as some tasks are just hard, for example, because the data is very noisy.

Always look at the data! Is there a pattern among wrong predictions, e.g., is there a discrepancy between the performance for different classes or do the wrongly predicted points have something else in common? Could some additional preprocessing steps help to fix errors for some type of data points (e.g., blurry images)?

Over- or underfitting is (partly) due to the model’s complexity:

While a simple model (e.g., a linear model) has a high bias and might therefore underfit the data, a more complex model (e.g., a deep neural network) has high variance and is therefore at risk of overfitting the training set. Often, it makes sense to use a more complex model, but then reduce its variance through explicit (e.g., L2-regularization) and/or implicit regularization (e.g., data augmentation). Also, please note the double descent phenomenon for neural networks, which often show a good generalization performance even if they are vastly over-parametrized.

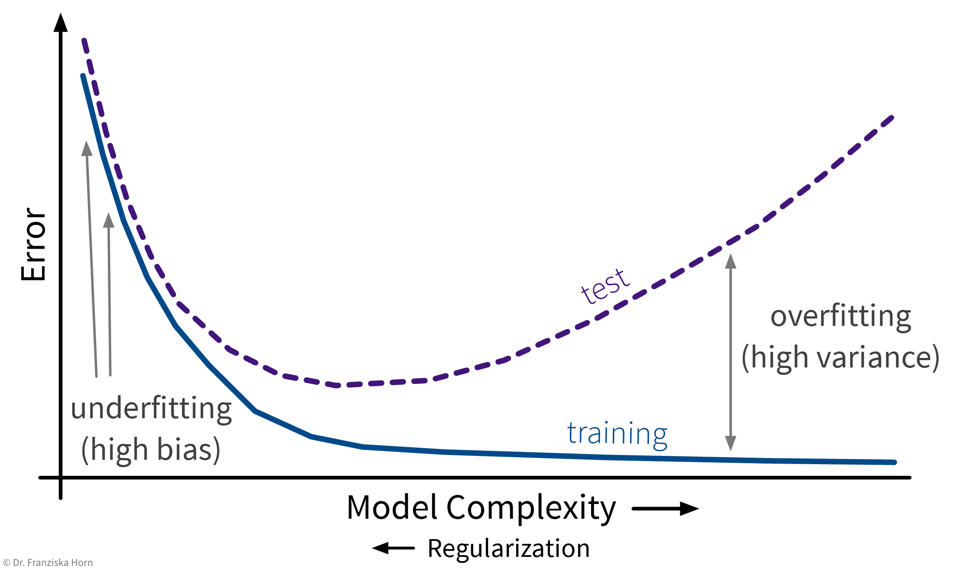
In general, one should first try to decrease the model’s bias, i.e., find a model that is complex enough and at least in principle capable of solving the task, since the error on the training data is the lower limit for the error on the test set. Then make sure the model doesn’t overfit, i.e., generalizes to new data points (what we ultimately care about).

Will more data help?: With little data, we risk overfitting. But is it worth getting more data?
→ check learning curves, i.e., how the performance improves when using more training samples:

Instead of more, it might also be helpful to get cleaner data, i.e., with less ambiguous labels! (See talk by Andrew Ng.)

For some tasks it is also possible to generate additional training samples programmatically through data augmentation, i.e., by modifying the original data points. For example, an image of an animal can be rotated or flipped without affecting its label. In this way we can easily increase the size of the training set without the need for human labeling. Furthermore, this makes our model more robust to realistic variations in the data. However, we need to be careful to not create garbage samples, i.e., a human must still be able of recognizing the objects in the images, for example.

Feature Selection

In small datasets, some patterns can occur simply by chance (= spurious correlations).
⇒ Exclude irrelevant features to avoid overfitting on the training data. This is especially important if the number of samples in the dataset is close to the number of features.

Feature selection techniques are either

unsupervised, which means they only look at the features themselves, e.g., removing highly correlated/redundant features, or
supervised, which means they take into account the relationship between the features and target variable.

Supervised Feature Selection Strategies:

1.) Univariate feature selection: e.g., correlation between feature & target

from sklearn.feature_selection import SelectKBest

Careful: This can lead to the inclusion of redundant features or the exclusion of features that might seem useless by themselves, but can be very informative when taken together with other features:

Guyon, Isabelle, and André Elisseeff. “An introduction to variable and feature selection.” Journal of Machine Learning Research 3.Mar (2003): 1157-1182.

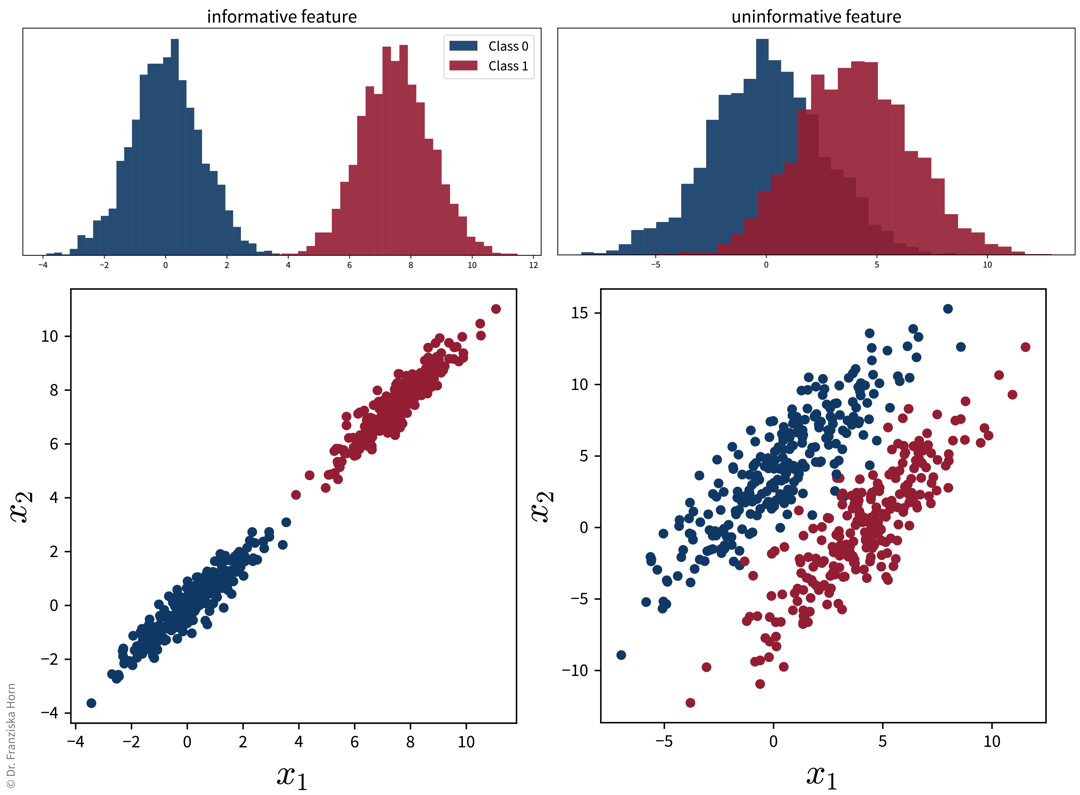
Also, please note: if we were to reduce the dimensionality with PCA on these two datasets, for the plot on the right, the main direction of variance does not capture the class differences, i.e., while the second PC captures less variance overall, it capture the class-discriminative information that we care about.

⇒ Better:

2.) Model-based feature selection: select features based on coef_ or feature_importances_ attribute of trained model

from sklearn.feature_selection import SelectFromModel

3.) Sequential feature selection

greedy algorithm that iteratively includes/removes one feature at a time:

forward selection: start with no features, iteratively add best feature until the performance stops improving
backward elimination: start with all features, iteratively eliminate worst feature until the performance starts to deteriorate

from sklearn.feature_selection import SequentialFeatureSelector

General rule: Always remove truly redundant (i.e., 100% correlated) features, but otherwise if in doubt: keep all features.

While feature selection can improve the performance, these automatic feature selection techniques will only select a subset of features that are good predictors of the target, i.e., highly correlated, not necessary variables that correspond to the true underlying causes, as we will discuss in the next section.