A Practitioner’s Guide to Machine Learning

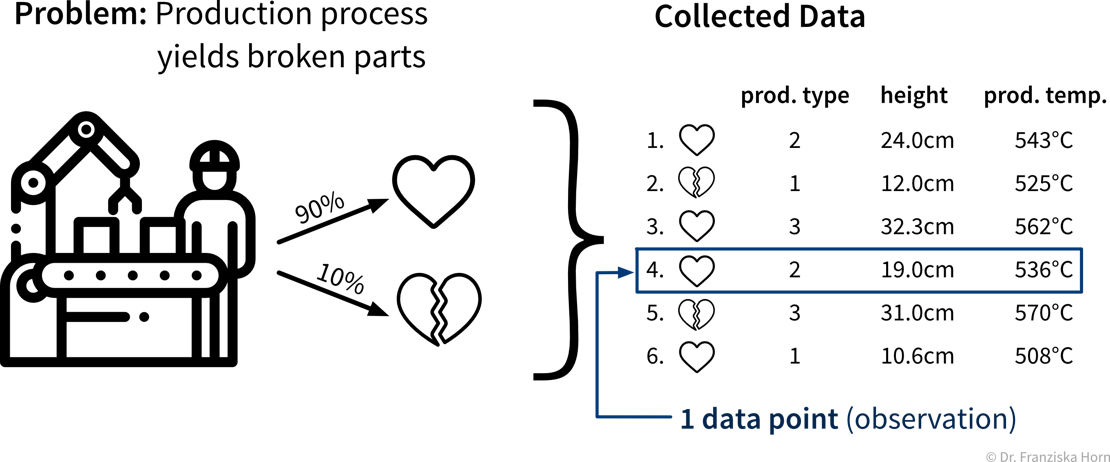
How do machines “learn”?

How do ML algorithms solve these “input → output” problems, i.e., how do they recognize patterns and learn rules from data?

The set of ML algorithms can be subdivided according to their learning strategy. This is inspired by how humans learn:

Unsupervised Learning: Humans are very good at picking up on statistical regularities in the world without being explicitly instructed to do so. For example, have you ever noticed that we don’t … make … pauses … between … words when we speak? Yet kids still intuitively learn which syllables make up a word and where this word ends and the next one begins. This is possible, because the syllables in a single word always occur in this specific combination, while this word can then be followed by many different words, starting with many different syllables. This means, simply by hearing lots of spoken text, we pick up on the conditional probability distributions of syllables. Supervised Learning: This type of learning requires a teacher that tells us what the right answers are and corrects us, if we get something wrong. For example, when teaching a kid the meaning of a word, we explicitly tell them what this word means, and if they mislabel something, e.g., call a small dog a cat, we correct them. Reinforcement Learning: This kind of learning-by-doing again happens naturally when humans learn from the consequences of their actions. For example, through experimentation and practice, we can figure out a complex sequence of hand movements to elicit beautiful sounds from a violin instead of producing painful screeches. While no single hand movement by itself is inherently good or bad, only the right combination will bring music to our ears.

Analogously, machines can also learn by following these three strategies:

Unsupervised Learning: These algorithms pick up on statistical regularities in the data, for example, they can find groups of similar items (like in the customer segmentation task) or identify individual points that stand out (i.e., anomaly detection), e.g., unusual behavior of a machine due to a broken part or suspicious credit card transactions. Supervised Learning: These algorithms learn from many input-output examples, e.g., images and what is shown on these images or production conditions and whether the product that was produced under these conditions is faulty or okay. The learned model can then be used to predict the output for some new input. Reinforcement Learning: This type of learning is a bit more involved: Here the learning algorithm is also called an agent, which operates within an environment, e.g., a robot moving around in the real world or a virtual agent inside a simulation environment like a video game (which is usually much cheaper ;-)). The environment lets the agent know in which state or situation it currently is, then the agent can select how to react in this state, i.e., which (predefined) action to take, and then the environment determines the consequences of this action (e.g., kill a monster in a video game or fall off a cliff) and returns a reward depending on the outcome (e.g., extra points for collecting coins). Then the cycle repeats as the agent is in the next state. Based on the received reward, the agent learns over time which actions are beneficial in which situations and how to navigate the environment. The hard part here is that the reward signals often come much later after the action was executed, for example, in a video game, an agent collects a key at the beginning of a level, but the door that can be opened with this key comes many frames later, which means the reward will be delayed and the agent has a hard time associating this reward with the appropriate action. Since humans have a lot of background knowledge, figuring out what works and what doesn’t in a game is much easier for us.

Data requirements for learning according to these strategies:

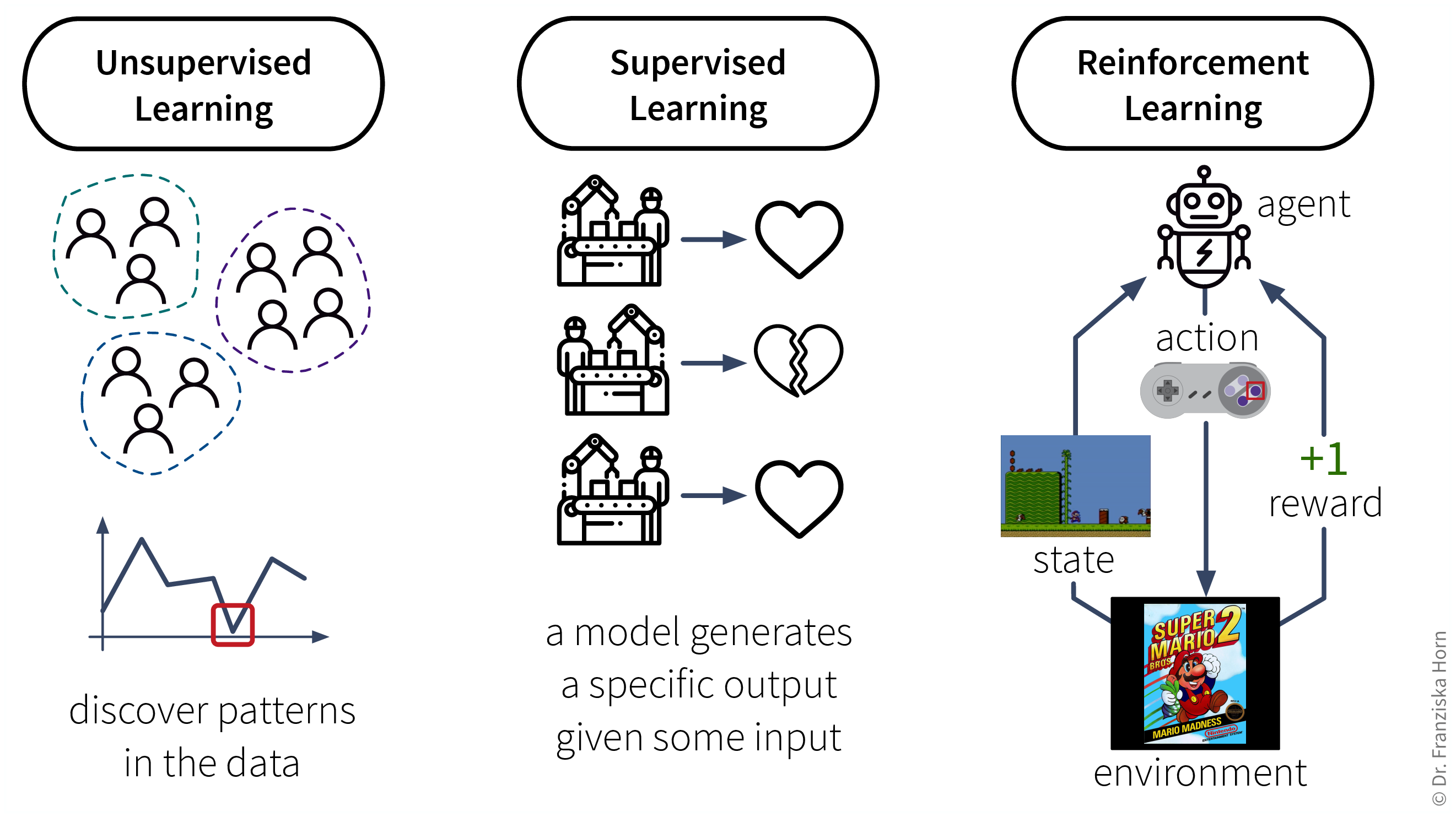
Unsupervised Learning: a dataset with examples
Supervised Learning: a dataset with labeled examples
Reinforcement Learning: a (simulation) environment that generates data (i.e., reward + new state) in response to the agent’s actions

With its reliance on a data-generating environment, reinforcement learning is a bit of a special case. Furthermore, as of now it’s still really hard to get reinforcement learning algorithms to work correctly, which means they’re currently mostly used in research and not so much for practical applications.

Supervised Learning

Supervised learning is the most common type of machine learning used in today’s applications.
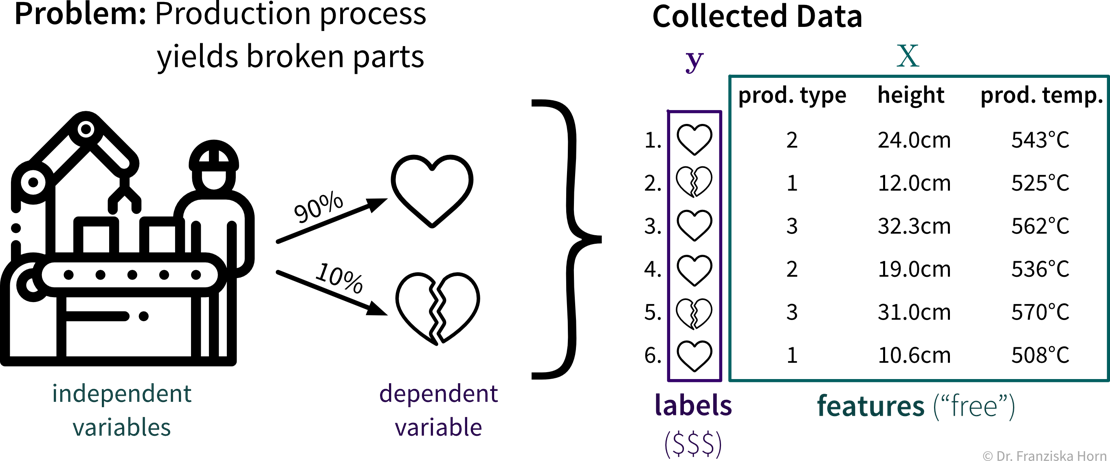
The goal here is to learn a model (= a mathematical function) \(f(x)\) that describes the relationship between some input(s) \(x\) (e.g., different process conditions like temperature, type of material, etc.) and output \(y\) (e.g., resulting product quality).
This model can then be used to make predictions for new data points, i.e., compute \(f(x') = y'\) for some new \(x'\) (e.g., predict for a new set of process conditions whether the produced product will be of high quality or if the process should be stopped to not waste resources).

Supervised Learning in a nutshell:: Before we start, we need to be very clear on what we want, i.e., what should be predicted, how will predicting this variable help us achieve our overall goals and create value, and how do we measure success, i.e., what is the Key Performance Indicator (KPI) of our process. Then, we need to collect data — and since we’re using supervised learning, this needs to be labeled data, with the labels corresponding to the target variable that we want to predict. Next, we “learn” (or “train” or “fit”) a model on this data and finally use it to generate predictions for new data points.

Features & Labels

A production process, where we want to predict whether a produced part is scrap given certain production conditions, is an example of a typical supervised learning problem. Here, the collected data for each produced part includes the process conditions under which it was produced, as well as the outcome, i.e., whether the product was okay or scrap:

The data collected for this use case is structured data in a tabular form (e.g., in an excel sheet). One data point / sample / observation is always in one row of this table.

The columns of the table contain the different measurements / variables that were collected for each sample. Here we distinguish between features (in this case the production conditions) and labels (whether the product produced under these conditions is okay or scrap). Features, also denoted as a matrix \(X\), are typically those measurements that we get basically for free, as they are often collected during the process for other purposes anyways. For example, when the operator of the machine sets the temperature for the production to a certain value, this is recorded as the signal is passed along to the heating unit. The corresponding labels, denoted as a vector \(\mathbf{y}\), are often more expensive to collect. For example, in the production process, to collect a data point with the label "scrap", we have to (intentionally) produce a broken product, costing us valuable resources. Another example: Google had to pay a team of specialist doctors to discuss and re-label some of the diabetic retinopathy images about which there existed conflicting opinions.

In the supervised learning setup, the features are used as the input to the model, while the labels constitute the target variable, i.e., the predicted output. Generally, features should be independent variables (e.g., settings that the operator can choose as he wishes), while the target value should be dependent on these inputs — otherwise we can’t predict it from these inputs alone.

“Learning” a model from the data

Goal: Describe the relationship between input(s) \(x\) and output \(y\) with a model, i.e., a mathematical function \(f(x)\)

Select a model class (= structure of the function): Assumption: relationship is linear
→ linear regression model: \(y = f(x) = b + w\cdot x\)
Define an objective: Minimize error between true & predicted \(y\):
→ \(\min_{b,w} \sum_i (y_i - f(x_i))^2\)
Find best model parameters given the data: i.e., solve the optimization problem defined in step 2
⇒ \(f(x) = -2.7 + 5.2x\)

Video Recommendation: If you’re not familiar with linear regression, the most basic supervised learning algorithm, please watch the explanation from Google decision scientist Cassie Kozyrkov on how linear regression works: [Part 1] [Part 2] [Part 3]

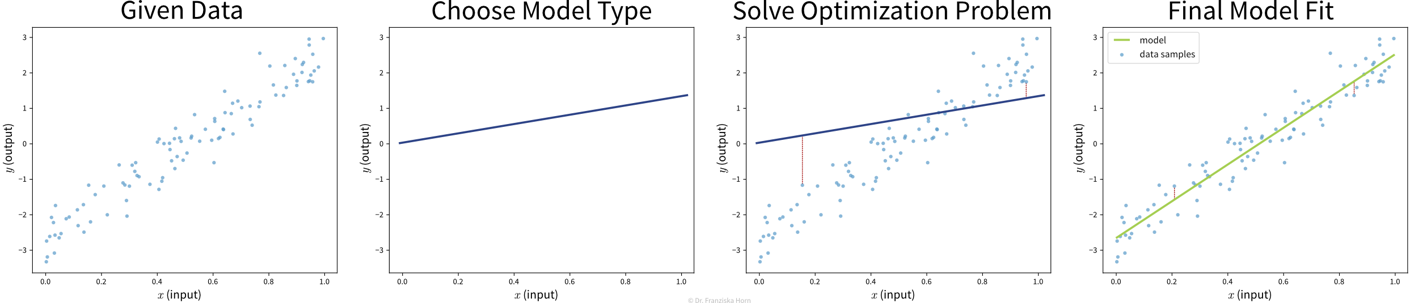
The available supervised learning algorithms differ in the type of \(x \to y\) relationship they can describe (e.g., linear or nonlinear) and what kind of objective they minimize (also called loss function; an error computed on the training data, quantifying the mismatch between true and predicted labels). The task of a data scientist is to select a type of model that can optimally fit the given data. The rest is then taken care of by an optimization method, which finds the parameters of the model that minimize the model’s objective, i.e., such that the model’s prediction error on the given data is as small as possible.

In most of the book, the terms “ML algorithm” and “ML model” will be used interchangeably. To be more precise, however, in general the algorithm processes the data and learns some parameter values. These parameter settings define the final model. For example, a linear regression model is defined by its coefficients (i.e., the model’s parameters), which are found by executing the steps outlined in the linear regression algorithm, which includes solving an optimization problem.

Don’t stop there!

In many use cases, it is not enough to “only” predict the target for a new data point, e.g., predict whether a product produced under certain conditions will be of high quality or not. Instead, it is often necessary to additionally be able to explain why this prediction was made, e.g., which input feature values were the deciding factors, both to better understand possible root causes of a problem, but also to be assured that the model is basing its predictions on reasonable assumptions. Furthermore, a learned model can also be used within an outer optimization loop, i.e., in the simplest case one could systematically check what product quality the model predicts for different process conditions and then select the settings with the highest predicted quality to produce new products. But keep in mind that ML models are only built to interpolate, not extrapolate, i.e., make sure the settings that are tested are withing the training domain.

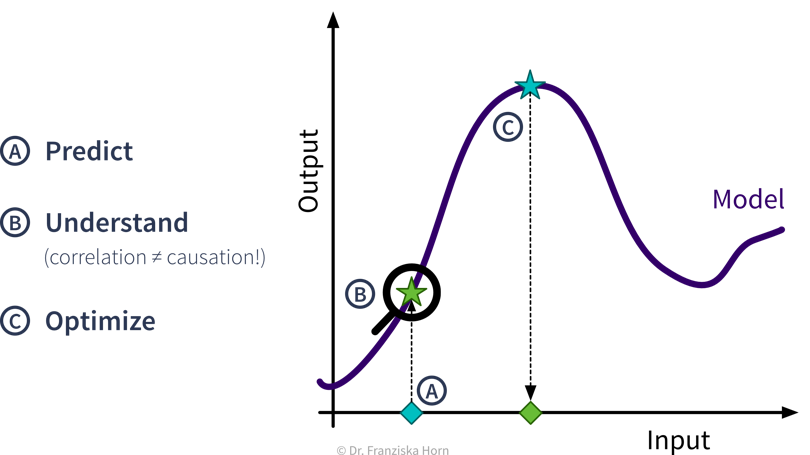
Predictive Analytics: By feeding historical data to a supervised learning algorithm, we can generate a predictive model that makes predictions about future scenarios to aid with planning.
Example: Use sales forecasts to better plan inventory levels.
Interpreting Predictive Models: Given a model that makes accurate predictions for new data points, we can interpret this model and explain its predictions to understand root causes in a process.
Example: Given a model that predicts the quality of a product from the process conditions, identify which conditions result in lower quality products.
What-if Analysis & Optimization: Given a model that makes accurate predictions for new data points, we can use this model in a “what-if” forecast to explore how a system might react to different conditions to make better decisions (but use with caution!).
Example: Given a model that predicts the remaining lifetime of a machine component under some process conditions, simulate how quickly this component would deteriorate if we changed the process conditions.

Going one step further, this model can also be used inside an optimization loop to automatically evaluate different inputs with the model systematically to find optimal settings.
Example: Given a model that predicts the quality of a product from the process conditions, automatically determine the best production settings for a new type of raw material.